信息增益的计算
对于如下数据集(feature为grade, bumpyness,speed limit, label为speed)
| grade | bumpiness | speed limit? | speed |
|---|---|---|---|
| steep | bumpy | yes | slow |
| steep | smooth | yes | slow |
| flat | bumpy | no | fast |
| steep | smooth | no | fast |
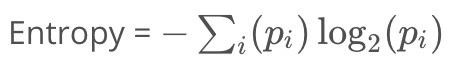
- 如果所有的样本是同一类,他的entropy(熵)为0
- 如果所有样本被均匀分散到所有可用类中,他的entropy为1
计算熵
 p(slow) = 2/4= 0.5
p(slow) = 2/4= 0.5
p(fast) = 2/4= 0.5
该节点的entropy为
entropy(node) = -p(slow)*log(p(slow)) - p(fast)*log(p(fast))
= -0.5* log(0.5) - 0.5 * log(0.5)
= 1.0

- steep节点的entropy 计算过程如下:
entropy(steep) = -p(slow)*log(p(slow)) - p(fast)*log(p(fast)) = -2/3* log(2/3) -1/3 * log(1/3) = 0.9184 - flat节点的entropy 为0
如果所有的样本是同一类,他的entropy(熵)为0
所以,
entropy(children) = 3/4 * entropy(steep) + 1/4 * entropy(flat)
= 3/4 * 0.9184 + 1/4 * 0
= 0.6888
计算信息增益
decision tree算法的目标是 最大化信息增益

信息增益为:父节点的entropy 减去子节点的entropy
information_gain= entropy(node) - entropy(children) = 1.0-0.6888 = 0.3112
同理计算得出:通过bumpyness切分时,获取到的信息增益为0;通过speed limit切分时,获取的信息增益为1
所以:我们应该选择speed limit来作为切分条件。
优缺点:
优点:
- 可解释性好
- 只需要很少的数据预处理工作。并且能够处理各种类型的特征
- 原生支持多分类
缺点:
- 决策树容易过拟合
- 决策树不稳定,也就是说可能数据集的一个很小的变动就会导致树发生很大的改变。
- 构建一个最佳的决策树是一个NP-hard问题,现有的启发式算法不能够保证最优(也没有一个理论的上下界)。
- 简单的决策树模型比较简单,很难表示数据集中的复杂关系